初一上学期期末试卷,初一数学期末考试卷及答案

　　大家好，我是陪娃学数学的老爸，今天再来分享一道七年级上学期数学期末试题。这是一道比较复杂的动角问题，也是需要分区间进行讨论。我们还是分享一下如何通过分析角度变化关系来解决。

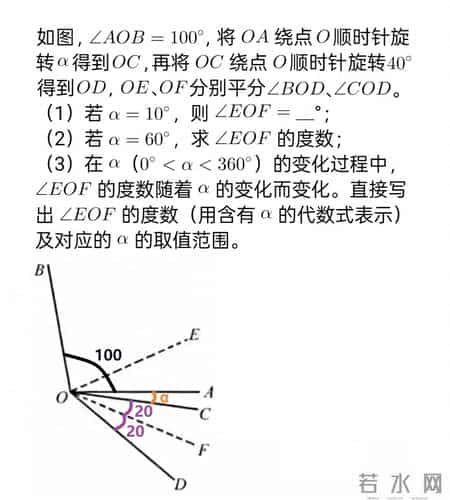
　　题目

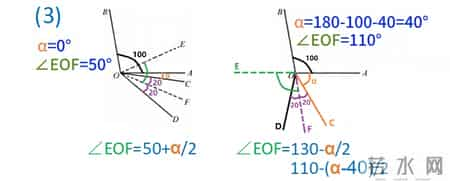
　　题目是说角AOB等于100度，OA顺时针旋转，先旋转阿尔法得到OC再继续旋转40度得到OD。OE和OF分别平分角BOD和角COD，也就是角COD的角度是40度固定不变的，平分后得到2个20度角。

　　第一小问是已知阿尔法等于10度，求角EOF。可以看出所求角就是平分后得到的角DOE减去平分后得到的角DOF。可以推出就等于角BOC的一半，也就是100度的角AOB加上阿尔法之和的一半，得到等于50加二分之阿尔法。阿尔法为10时，算出等于55度。

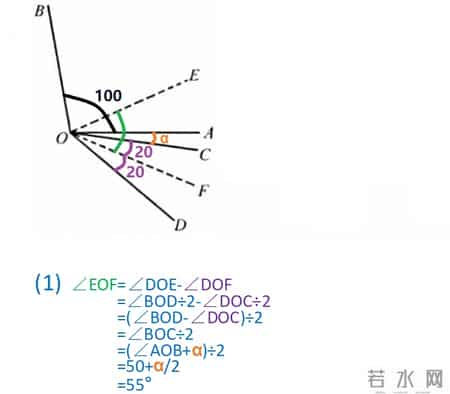
　　第1小问

　　第二小问是阿尔法等于60度，求角EOF。画出大致的位置，此时100度加阿尔法加40度等于200度，已经超过了180度，所以角BOD的平分线OE就位于BOD的左侧。角度关系也和上一小问中的位置有变化，所求角等于平分后得到的角DOE加上平分后得到的角DOF。推出等于360度减角BOC再除以2，即等于130减二分之阿尔法。阿尔法为60时，算出等于100度。

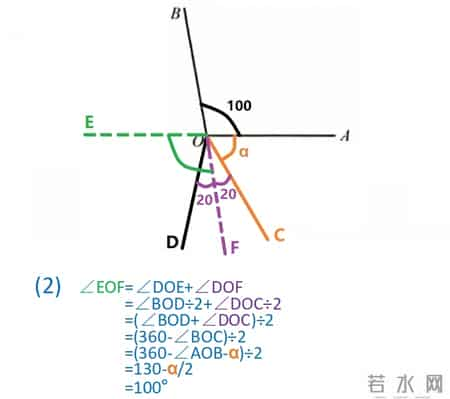
　　第2小问

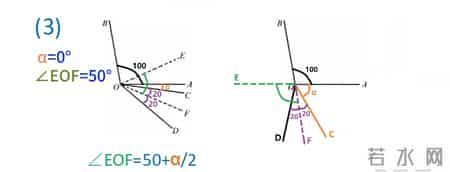
　　第三小问是阿尔法从零增加至360度的过程中用含阿尔法的代数式表示角EOF，并写出对应的阿尔法取值范围，也就是需要对阿尔法分段讨论。

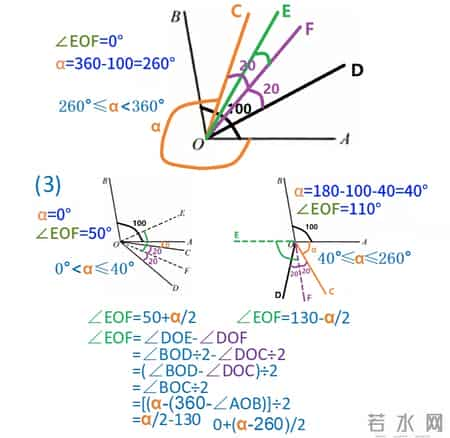
　　我们可以参照一下前两个小问中的位置。当阿尔法从零开始增加时，所求角为角DOE减角DOF。阿尔法在起始点0度时，所求角等于50度。其中角DOF度数固定不变。角DOE的增加量是角阿尔法增加量的一半，也就是所求角也是逐渐增加的。那么这段区间的表达式就是第一小问中已经得到的，所求角等于50加二分之阿尔法。通过角度变化量理解的话，就是初始值50度，加上阿尔法增加量的一半。

　　第1小问位置对应的分段区间一

　　这个变化趋势一直到角BOD等于180度为止，也就是这之后OE会跳变到BOD的左侧。对于阿尔法来说的跳变点就是阿尔法等于180度减100减40等于40度。在临界点时所求角等于角DOE加角DOF，等于90加20等于110度。这之后随着阿尔法的增大，角DOF度数仍然固定不变，角DOE逐渐减小，减小量是阿尔法增加量的一半，这段区间的表达式就是第二小问中已经得到的，所求角等于130减去二分之阿尔法。通过角度变化量理解的话，就是初始值110度减去阿尔法相对于临界点40度的增加量的一半，也是同样的结果。这个区间的结束点我们还要继续分析一下。

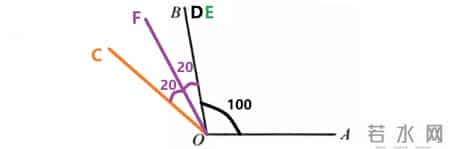
　　第2小问位置对应的分段区间二

　　首先OD达到OB的位置，这时角DOE已经减至最小的零度。继续旋转的话角DOE就会变成逐渐增大。可能有孩子会觉得这就是一个分界点。实际上这之后虽然角DOE变成逐渐增大，但是所求角的表达式也发生了变化，由原来的角DOF和角DOE相加变成了相减。也就是随着角DOE的增加，所求角仍然是逐渐减小的，变化趋势并没有变，相当于原来算式中增加的角变成了负数，所以OD和OB重叠的位置并不是一个分界点。

　　角DOE为0时

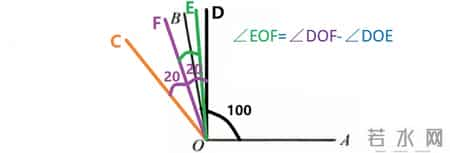
　　角DOE变成0后又开始逐渐增大

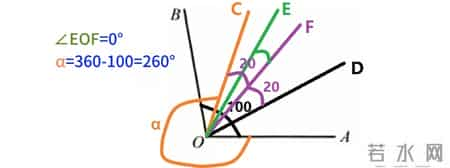
　　所以继续旋转一直到所求角减小为零度即OC和OB重叠的位置。这时候阿尔法对应的度数为360度减100等于260度。

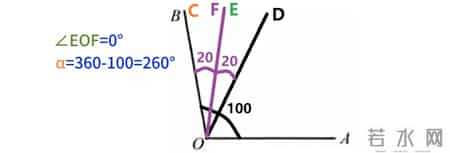
　　所求角EOF为0时

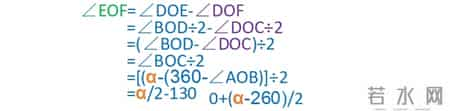
　　这之后随着阿尔法的增加，角DOF度数仍然不变，角DOE逐渐增加，增加量是阿尔法增加量的一半。那么所求角等于角DOE减角DOF也是逐渐增加的。这个趋势一直保持到阿尔法增大为360度截止。这段区间，所求角的表达式推出也等于角BOC除以2。最终得到等于2分之阿尔法减130。通过角度变化量理解的话，就是初始值零度加上阿尔法相对于临界点260度的增加量的一半，可以得到同样的结果。

　　区间三

　　区间三角度关系

　　最后我们再把阿尔法的取值范围补充一下。第一个区间的截止点是角BOD等于180度，且阿尔法等于40度的位置，所以区间为0到40度。第二个区间的截止点为OC和OB重叠的位置，即阿尔法等于260度，所以区间为40度到260度。第三个位置的区间就是260度到360度。

　　三个区间

　　以上就是对这道题的分享，希望对大家有所帮助。

　　该内容为视频文稿，查看原视频：

　　【七年级初一上学期数学题，期末试题，通过分析角度变化关系解决复杂的动角问...】

　　点击链接打开 https://m.toutiao.com/is/4F1OSlM2YIw/ 4F1OSlM2YIw` igT:/ q@e.Ox :8am